Unity►游戏

A* 算法

游戏中常常有寻路的说法，因为路径很复杂的话，就要考虑算法问题。A*是常用的算法。
虽然很多时候我们用到插件，明白一些理论，但是从未实现过。
今天用老迷宫问题来实现下这个经典算法。

看下理论：A算法；A（A-Star)算法是一种静态路网中求解最短路径最
有效的直接搜索方法，也是解决许多搜索问题的有效算法。
算法中的距离估算值与实际值越接近，最终搜索速度越快。

先用代码实现一下，再抄篇原理就好了。

实验

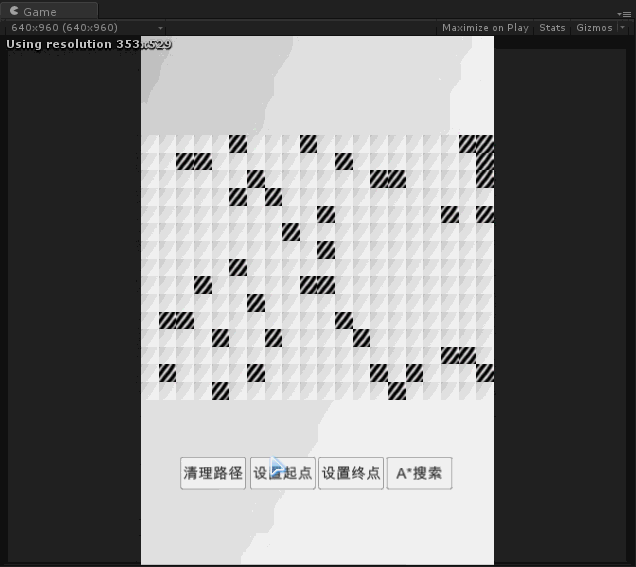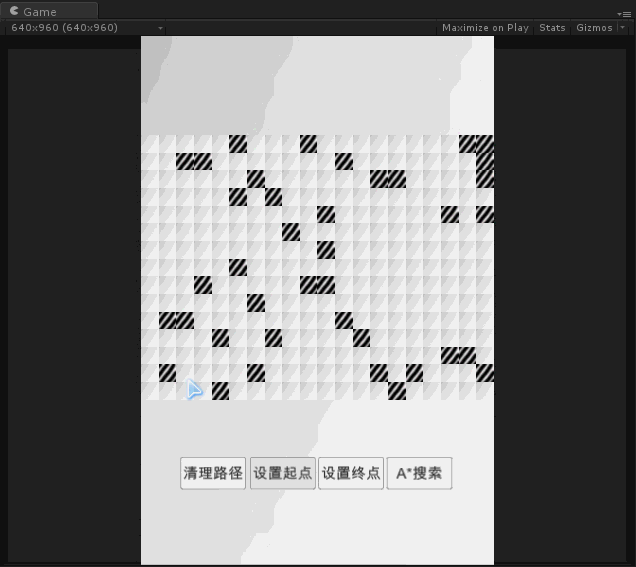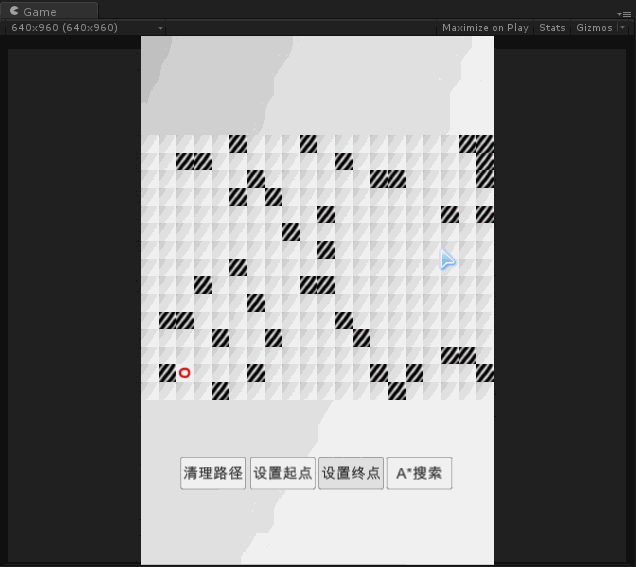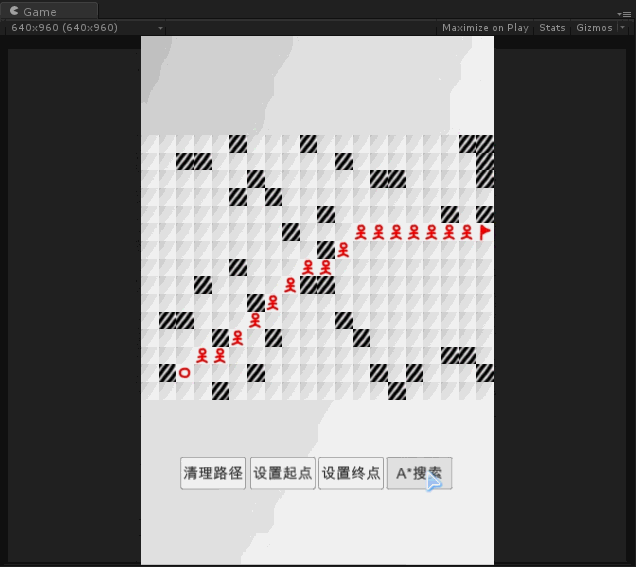
代码下载:

AStar.rar

主要逻辑代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
public MazeContent OnSearchAStar(MazePoint begin, MazePoint end, System.Func<IMazeContentObject, bool> func) {
    //搜索处理下标志值等，环境
    Loop((e) => { e.BeforeSearch(); });

    MazeContent mbegin = map[begin.x, begin.y];
    MazeContent mend = map[end.x, end.y];

    //把begin点放open表
    MazeContent queue = pushOpen(null, mbegin);

    while (queue != null) {
        MazeContent head;
        //依次取open表的最小权重的点n
        queue = popOpen(queue, out head);

        //如果达到目标
        if (head == mend) return head;

        //沿8方面查找
        for (int i = 0; i < 8; ++i) {
            int dx = head.X + tx[i];
            int dy = head.Y + ty[i];
            
            //越界检查
            if (dx < 0 || dx >= maxLine || dy < 0 || dy >= maxColumn) continue;

            //权重计算：这里函数用的不好
            float fx = (dx - mend.X) * (dx - mend.X) + (dy - mend.Y) * (dy - mend.Y);
            MazeContent m = map[dx, dy];

            if (!func(m.item)) continue;
            
            // 更新open中的x点：用小的权重代替
            if (m.IsOpen) {
                if (fx < m.G) {
                    m.Parent = head;
                    m.G = fx;
                }
                continue;
            }

            // 已经被搜索处理过了
            if (m.IsClose) continue;

            // 放open表
            // if (!m.isopen && !m.isclose)
            m.Parent = head;
            m.G = fx;
            queue = pushOpen(queue, m);
        }
        // 放close表
        pushClose(head);
        // 排序queue,优化的关键
        queue = sort(queue);
    }

    return null;
}

原理

A*算法是一种静态路网中求解最短路最有效的直接搜索方法，也是许多其他问题的常用启发式算法
，比如其他预处理算法（ALT，CH，HL等等）。

公式表示为： f(n)=g(n)+h(n),
其中 f(n) 是从初始状态经由状态n到目标状态的代价估计，
g(n) 是在状态空间中从初始状态到状态n的实际代价，
h(n) 是从状态n到目标状态的最佳路径的估计代价。
（对于路径搜索问题，状态就是图中的节点，代价就是距离）

##h(n)的选取
保证找到最短路径（最优解的）条件，关键在于估价函数f(n)的选取（或者说h(n)的选取）。
我们以d(n)表达状态n到目标状态的距离，那么h(n)的选取大致有如下三种情况：

  • 如果h(n)<= d(n)到目标状态的实际距离，这种情况下，搜索的点数多，搜索范围大，效率低。但能得到最优解。
  • 如果h(n)=d(n)，即距离估计h(n)等于最短距离，那么搜索将严格沿着最短路径进行， 此时的搜索效率是最高的。
  • 如果 h(n)>d(n),搜索的点数少，搜索范围小，效率高，但不能保证得到最优解

##伪代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
while(OPEN!=NULL)
{
    从OPEN表中取f(n)最小的节点n;
    if(n节点==目标节点)
        break;
    for(当前节点n的每个子节点X)
    {
        计算f(X);
        if(XinOPEN)
            if(新的f(X)<OPEN中的f(X))
            {
                把n设置为X的父亲;
                更新OPEN表中的f(n);
            }
        if(XinCLOSE)
            continue;
        if(Xnotinboth)
        {
            把n设置为X的父亲;
            求f(X);
            并将X插入OPEN表中;//还没有排序
        }
    }//endfor
    将n节点插入CLOSE表中;
    按照f(n)将OPEN表中的节点排序;//实际上是比较OPEN表内节点f的大小，从最小路径的节点向下进行。
}//endwhile(OPEN!=NULL)